●ついでに「年率」のお作法の話をしておく

ほんとはもうこれで十分なんだけど、一応計算の続きの話をしておこうかな。あ、我が娘は気絶しそうだから置いていこう。よし、夫君と１対１で話そうじゃないか。

80万円が135万円になるのにちょうど１年だったとしたら、さっきの68.75％はそのまま「年利」になるよね。「年率」という言い方もする。「この投資のリターンは年率68.75%でした」って感じ。じゃあもし、10年かかって135万円になったんだとしたら、どう表現すべきだろうか。

そう、金融の慣習としては「年利に換算」するのが一般的なんだよね。銀行の預金金利もローン金利も一般的には「年率何パーセント」という言い方をするじゃない。そうやって同じモノサシで揃えることではじめて横比較ができるので、金融商品では「年率」がデフォルトなわけ。

さて、10年かかって68.75％になったこの投資は、いったい「年率何パーセント」なんだろうか。実はこの年率に換算する方法としても、また「単利」と「複利」というのが出てきてしまう。ただし今度は、さっき話した実際に出た利息の扱い方、リアルな運用方法の話とは違って、年率換算をする際の単なる計算上の仮定の話でしかない。

10年の68.75%という結果を年率に直すにあたって、「固定金利だと仮定した場合に、利息を運用しないで積んできた単利運用だったと仮定しますか、それとも利息を元本に組み入れる複利運用で増えてきたと仮定しましょうか」という話。実際には利息が出るわけでもなければ、価格上がったり下がったりした結果、10年後に135万円になっているだけなので単利も複利もないというのは既に話した通り。単に年率換算の計算をするために、どちらかに仮定を置きましょうね、という話だ。

具体的には、68.75%を10年だからと10で割り算した6.875%とするのが単利による年率換算で、ルート10するのが複利による年率換算だ。具体的には135÷80をルート10して1を引いた結果である5.372%となる。

あら、ホントに我が娘は寝たな。放っといて続けるわ。なぜルートをするかわかる？答えは、「10乗」で10年運用されたと仮定するから逆のルート10をする、なんだけど説明が必要だよね。

まず、80万円を年率何パーセントかの固定金利で運用したらどういう式になると思う？1年後には80万円＋「80万円×〇％」の金額になってるよね。式を簡単にすると80で括ってあげて「80×（1＋〇）」だよね。さてでは２年後は？複利運用だったと仮定するのだから、２年目はこの増えた金額にまた〇％の運用がされるとして（80×（１＋〇））×（1＋〇）と書けるよね。そして３年目はさらに――。

ということで、絵にするとこうなる。〇をリターンのｒと置いてみた。

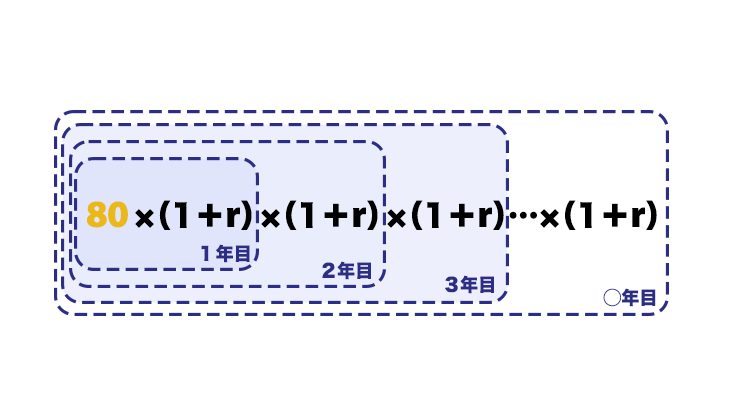
こんな風にして増えてきた80万円が10年後にいくらになったんだっけ？135万円だったよね。つまりこういう式になる。

これを展開してｒを求めよう。それが複利換算の年率リターンだ。

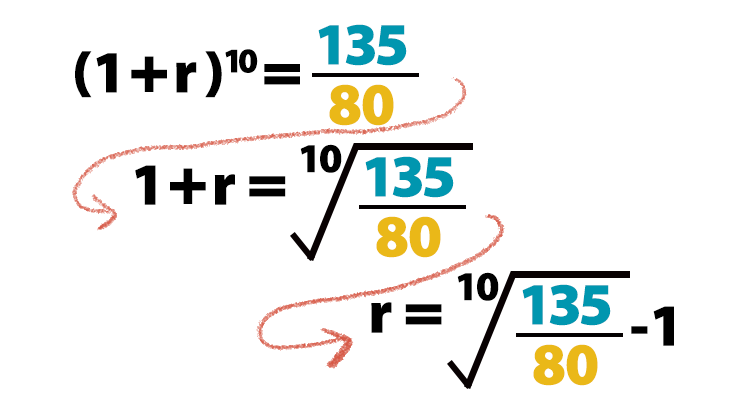
こうやって求めたｒの値が、さっき言った5.372%だったわけ。ルート10なんて手計算できないから、もちろんエクセルでさっき計算しといたの。

整理しようかね。80万円が10年後に135万円になった投資の結果は、年数を考慮しない計算だと135÷80－1＝68.75％のリターンとなる。金融の作法である年率でそれを表現すれば、簡便法としての単利換算なら「÷10」をした6.875%／年であり、金融のデフォルトである複利換算ならルート10した5.372%／年となる。

ひとつ気付いてほしいのは、年率換算の値は常に単利換算（6.875%）よりも複利換算（5.372%）の方が値が小さくなることだ。これは計算を行なう際に複利という、単利に比べて増え方が速い方法を仮定したのだから当たり前のこと。より小さいパワーでも同じ135万円まで増える方法を計算の前提に置いたから、ということだね。

次ページへ＞